$\newcommand{\E}{\mathbb{E}}$ $\newcommand{\argmax}{\mathrm{argmax}}$ $\newcommand{\Mu}{M}$ $\newcommand{\ba}{\bar{a}}$ $\newcommand{\hx}{\hat{x}}$ $\newcommand{\argmin}{\mathrm{argmin}}$ $\newcommand{\sigmasqr}{\sigma^2}$ This article synthesizes insights from multiple original research papers and both English and Chinese academic sources, with original analysis and derivations by the author.

Todo list

• Translate to Markdown
• Check Equations
• Fix Image & Website References

1. Problem Settings

The goal is to quickly solve:

\[\argmin_p F(x,p) = \int_0^T f(x,p,t) \, dt\]

Naturally, we use gradient descent, so we need a fast estimation of $ \nabla_p F(x,p) $, which will be abbreviated as $ d_p F(x,p) $. Note that there are PDE constraints (general form):

\[\frac{dx}{dt} = \dot{x} = \bar{h}(x,p,t) \quad \Rightarrow \quad h(x,\dot{x},p,t) = 0\]

and an integral initial condition constraint:

\[g(x(0),p) = 0\]

2. Adjoint Method (1st Order)

Clearly, we have:

\[d_p F(x,p) = \int_0^T \left[\partial_x f d_p x + \partial_p f \right] \, dt\]

Considering the Lagrangian equation under the constraint, where the parameters are $ \lambda $ and $ \mu $, we have:

\[\mathcal{L} = \int_0^T \left[f(x,p,t) + \lambda^T h(x,\dot{x},p,t)\right] \, dt + \mu^T g(x(0),p)\]

where $ \lambda $ is a function of time. Differentiating gives:

\[d_p \mathcal{L} = \int_0^T \left[ \partial_x f d_p x + \partial_p f + \lambda^T \left( \partial_x h d_p x + \partial_{\dot{x}} h d_p \dot{x} + \partial_p h \right) \right] \, dt + \mu^T \left( \partial_{x(0)} g d_p x(0) + \partial_p g \right)\]

Now, let’s focus on the fourth term in the integral:

\[\int_0^T \lambda^T \partial_{\dot{x}} h d_p \dot{x} \, dt\]

Noticing that:

\[d_p \dot{x} = \frac{d}{dp} \left( \frac{dx}{dt} \right) = \frac{d}{dt} \left( \frac{dx}{dp} \right)\]

we assume continuous partial derivatives. Then, we perform integration by parts to obtain:

\[\lambda^T \partial_{\dot{x}} h d_p x \bigg|_0^T - \int_0^T \left[\dot{\lambda}^T \partial_{\dot{x}} h + \lambda^T d_t \partial_{\dot{x}} h \right] d_p x \, dt\]

Substituting this back into the original expression, we get:

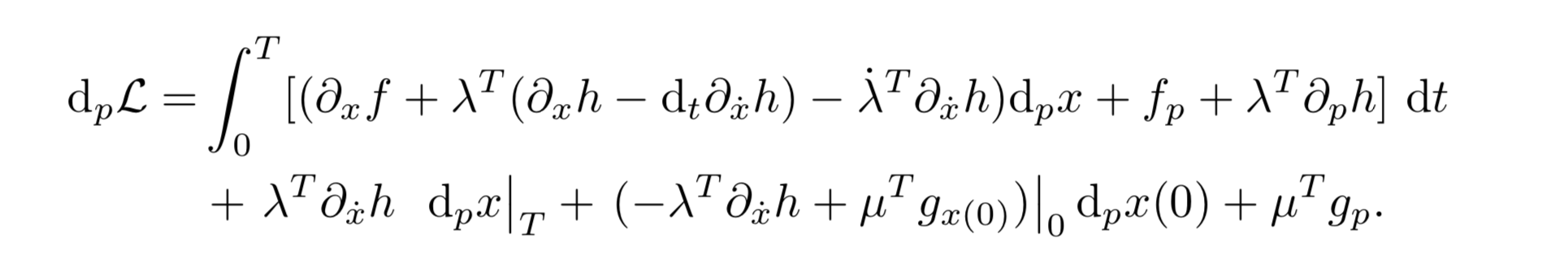
Notice that the first term from the integration by parts is split. Since $ \lambda, \mu $ are arbitrary, and to avoid the computation of the complex $ d_p x\vert_T $ (which is a Jacobian), we set:

\[\lambda(T) = 0\]

Similarly, we define:

\[\mu^T = \lambda^T(0) \partial_{\dot{x}} h(0) g_{x(0)}^{-1}\]

This removes the last two terms. To avoid computing any $ d_p x $ in the integral, we select $ \lambda $ such that:

\[f_x + \lambda^T (h_x - d_t h_{\dot{x}}) - \dot{\lambda}^T h_{\dot{x}} = 0\]

Thus, we have:

\[d_p \mathcal{L} = \int_0^T \left[ f_p + \lambda^T h_p \right] \, dt + \lambda^T(0) h_{\dot{x}}(0) g_{x(0)}^{-1} g_p\]

Since the Lagrangian function at the minimum is the same as the original constraint, we only need to use the gradient of this function for descent. Therefore, we can set:

\[d_p F = d_p \mathcal{L}\]

Then:

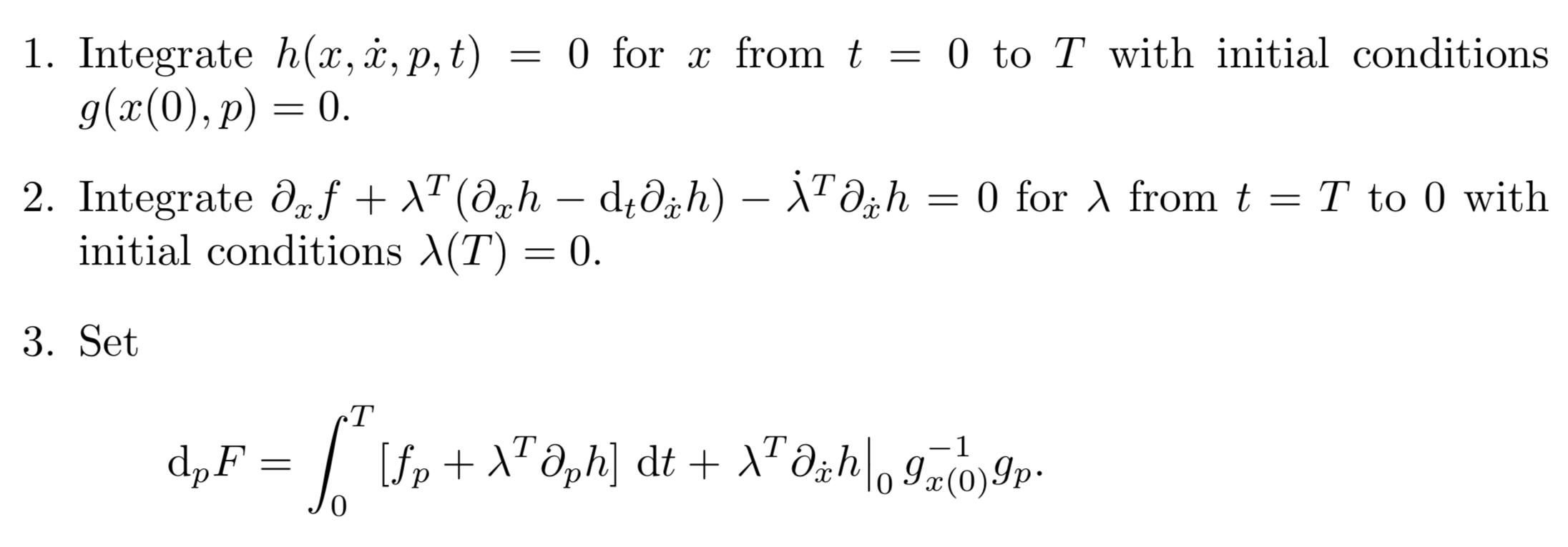
3. Adjoint Method with Neural ODE

Reviewing the approach for Neural ODE:

\[\mathcal{L}(z(t)) = \mathcal{L} \left( z(t_0) + \int_{t_0}^{t_1} f(z(t), t, \theta) \, dt \right)\]

The derivation gives:

\[\nabla_\theta \mathcal{L}(z(t)) = -\int_{t_N}^{t_0} \left( \frac{\partial \mathcal{L}}{\partial z(t)} \right)^T \frac{\partial f(z(t), t, \theta)}{\partial \theta} \, dt\]